Finding the Sweet Spot: Cost-Efficiency in LLM Production

TL;DR At ReflektLab, we're constantly balancing performance with economics. Our latest benchmark evaluated 9 LLMs across 1,260 tests, measuring not just accuracy, but cost per accuracy point, token efficiency, JSON quality, and production reliability across 10 runs per test. Instead of asking "which model is best?", we asked: how much can we save without compromising reliability?

What We Benchmarked

Premium tier: Claude Opus 4.5 (frontier model, high-cost reference - excluded from efficiency quadrant due to much higher cost)

Large open models: Meta Llama 3.3 70B Instruct, DeepSeek V3.2

Mid-range & compressed: GPT-4o-mini, Qwen3 14B, MiniMax M2.1, GLM-4.7 Flash, NVIDIA Nemotron Nano 9B

Tiny/compressed: Google Gemma 3N E4B IT (4B parameters)

Tasks focused on production-critical workloads: product extraction, complex JSON schema generation, and structured data parsing. Each test ran 10 times to measure production reliability, not just averages.

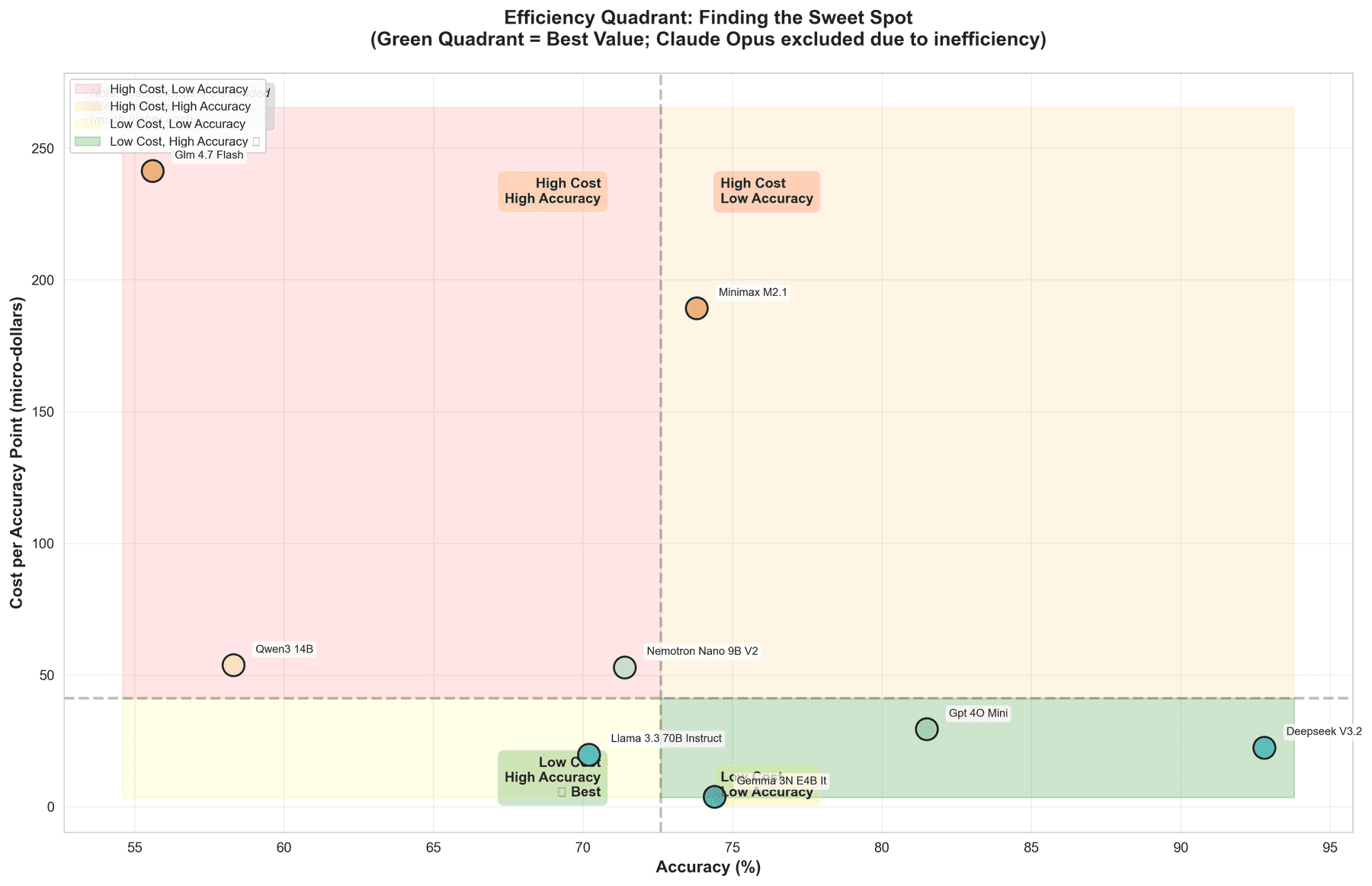
The Cost-Efficiency Landscape

Accuracy range: Models span from 55.6% to 92.8% accuracy, with DeepSeek V3.2 leading at 92.8% — but that's only part of the story.

Cost per accuracy point tells a different tale: Google Gemma 3N (4B) achieves 74.4% accuracy at just $0.00000370 per accuracy point — 390x cheaper than Claude Opus 4.5, which costs $0.00144456 per accuracy point despite only reaching 83.3% accuracy.

DeepSeek V3.2 emerges as the efficiency champion: 92.8% accuracy (highest in our test) at $0.00002240 per accuracy point — delivering premium-tier performance at mid-range costs.

Token efficiency reveals another dimension: DeepSeek V3.2 uses only 74.8 tokens per accuracy point, compared to GLM-4.7 Flash's 662.4 tokens per accuracy point — nearly 9x more verbose for lower accuracy (55.6%).

Methodology: Cost per accuracy point = total_cost ÷ accuracy_percentage, where accuracy is calculated as (passed_tests ÷ total_tests) × 100. For example, a model with $0.002 total cost and 74.4% accuracy yields $0.002 ÷ 74.4 = $0.00002688 per accuracy point. Tokens per accuracy point = total_tokens ÷ accuracy_percentage, where total_tokens includes both input (prompt) and output (completion) tokens.

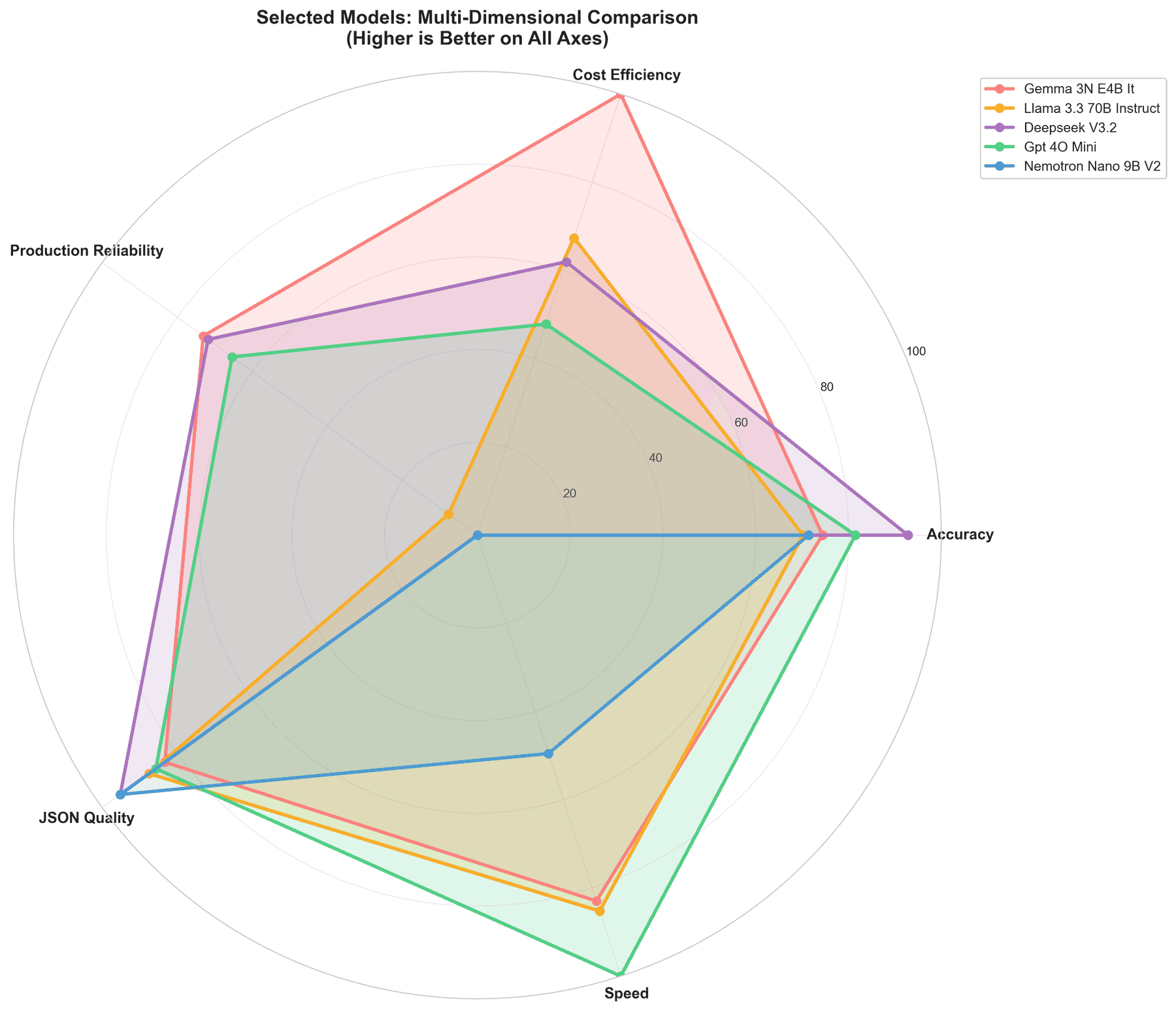
Key Insights

Production Reliability: The Hidden Cost of Variance

We measured coefficient of variation (CV) across 10 runs. Lower variance means predictable costs and fewer production surprises.

Most reliable: Google Gemma 3N (2.1% CV), DeepSeek V3.2 (2.2% CV), GPT-4o-mini (2.7% CV). These models deliver consistent results run-to-run, critical for production systems where cost predictability matters as much as average cost.

High variance models like GLM-4.7 Flash (16.4% CV, accuracy swings of 45.8%–72.7%) and Qwen3 14B (14.1% CV, accuracy swings of 45.8%–66.7%) show wide accuracy ranges across runs. This unpredictability can lead to unexpected costs and reliability issues in production.

JSON Quality: Beyond Accuracy

Valid JSON generation matters for production APIs. Qwen3 14B achieves 100% syntactically valid JSON (parseable) with 99.9% schema compliance (matching required structure) — the only model to hit perfect JSON parseability. DeepSeek V3.2 follows at 95.2% valid JSON with 95.1% schema compliance.

Several models struggle with complex JSON structures: Gemma 3N, Claude Opus, and MiniMax all hover around 83% valid JSON, which could require additional validation layers in production.

Cost vs. Performance: The Tiers

Budget tier (under $0.00002 per accuracy point):

• Google Gemma 3N: 74.4% accuracy, $0.00000370/point
• Meta Llama 3.3 70B: 70.2% accuracy, $0.00001974/point

Value tier ($0.00002–$0.0001 per accuracy point):

• DeepSeek V3.2: 92.8% accuracy, $0.00002240/point ⭐ Best balance
• GPT-4o-mini: 81.5% accuracy, $0.00002935/point
• NVIDIA Nemotron: 71.4% accuracy, $0.00005289/point

Premium tier (over $0.0001 per accuracy point):

• Claude Opus 4.5: 83.3% accuracy, $0.00144456/point (390x more expensive than Gemma)

A note on Claude Opus: Our binary pass/fail scoring may not fully capture Claude's nuanced capabilities. It sometimes produces alternative valid interpretations that our tests marked as incorrect, potentially understating its true accuracy. Its real-world performance on complex reasoning tasks may exceed the 83.3% shown here.

Latency: Speed vs. Cost

Fastest models: GPT-4o-mini (2.147s), Meta Llama 3.3 70B (3.381s), Google Gemma 3N (3.573s). Slowest: Qwen3 14B (14.431s), GLM-4.7 Flash (14.368s).

The trade-off: DeepSeek V3.2 is slower but delivers the highest accuracy at reasonable cost. GPT-4o-mini is fastest with good accuracy, making it ideal for latency-sensitive workloads. Gemma 3N offers the best cost/speed ratio for high-volume, lower-accuracy-tolerance use cases.

From Benchmark to Production Strategy

This benchmark reveals a clear tiered routing strategy:

Default path: Use DeepSeek V3.2 for high-accuracy needs ($0.00002240/point) or Gemma 3N for cost-sensitive, high-volume workloads ($0.00000370/point).

Latency-critical path: Route to GPT-4o-mini (2.147s average) when speed matters more than absolute accuracy.

JSON-critical path: Qwen3 14B achieves 100% valid JSON but shows high variance (14.1% CV) with accuracy swings of 45.8%–66.7% across runs, making it unsuitable for critical workloads. Use only for non-critical scenarios with strict safeguards: non-critical JSON validation, batch processing with retry logic, or as a secondary validator.

The Bottom Line

You don't need to pay premium prices for most production workloads. DeepSeek V3.2 delivers 92.8% accuracy at 1/65th the cost of Claude Opus 4.5. Google Gemma 3N (4B parameters) achieves 74.4% accuracy at 1/390th the cost — proving that smaller models can handle many production tasks effectively.

The key is measuring production reliability, not just averages. Models with low variance (CV < 5%) provide predictable costs and reliability, while high-variance models introduce hidden operational risks.

If you're optimizing LLM costs without sacrificing quality, these results show that a data-driven, tiered routing approach can reduce costs by 10–100x while maintaining production-grade reliability. The question isn't whether you can afford premium models — it's whether you can afford not to measure what you actually need.